New insights into COVID-19 modeling
Tue, 03/22/2022 - 7:33amThe COVID-19 pandemic has led to an unprecedented worldwide response to grapple with the fast spreading virus. Professors Cameron Browne and Hayriye Gulbudak and graduate student Joshua Caleb Macdonald have obtained some novel results modeling connections between disease proliferation and interventions to slow the spread of the disease.
In contrast to existing models that assume linear rates of population quarantine or time-dependent transmission rates, the nonlinear lockdown rate used in their models captures a contagion-like behavioral response to infected cases which allows them to derive novel formulas for final outbreak size.
This can be translated to a time of action for quarantine measures, analytically demonstrating the escalating impacts of delaying implementation of responsive lockdowns beyond a critical time period, which has been suggested in other studies based on simulations. For instance, as a rule of thumb, to reduce the outbreak size by 90%, the quarantine rate (or amount of self-quarantined in a defined time period) must be 9 times baseline R_0 times the rate (or amount) of incoming reported cases.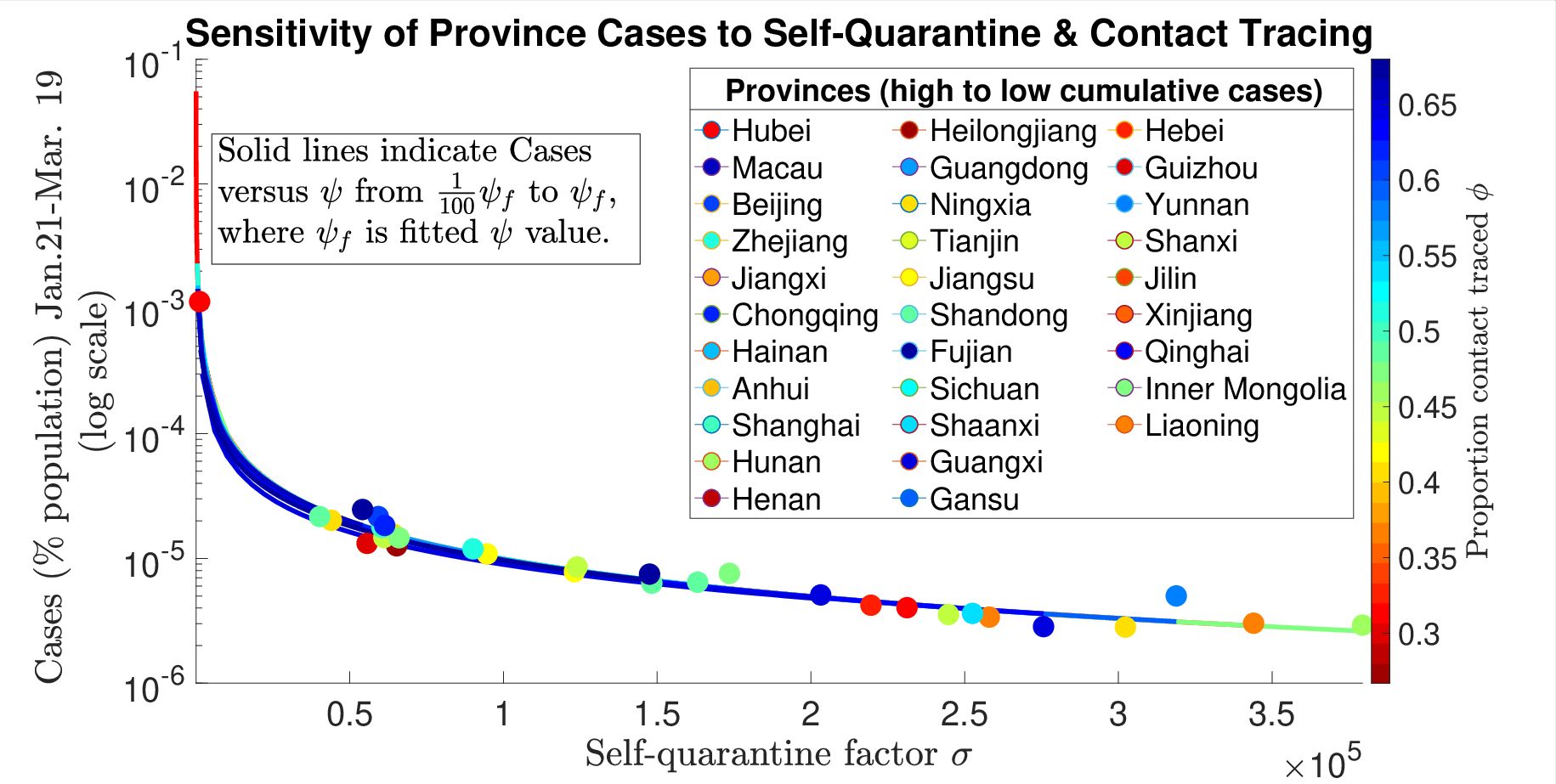
As noted above, public health and individual responses can lead to contagion-like behavioral responses to infected cases where the rate of population-wide self-quarantine behavior (or lockdowns) and the more targeted intervention of contact tracing are linked to case counts. By quantifying each of these reactionary quarantine measures in a mathematical model of COVID-19 epidemics, they analytically derived distinct nonlinear effects of these interventions on final and peak outbreak size. In particular, they found an inverse proportionality law between outbreak size and lockdown rate, whereas imperfect contact tracing has marginal impact on cumulative cases for infectious diseases with relatively high "reproduction number R_0". These findings were demonstrated when simultaneously fitting the model to case, mortality and contact tracing data from Chinese provinces allowing them to tease apart the differing intervention efficacies.
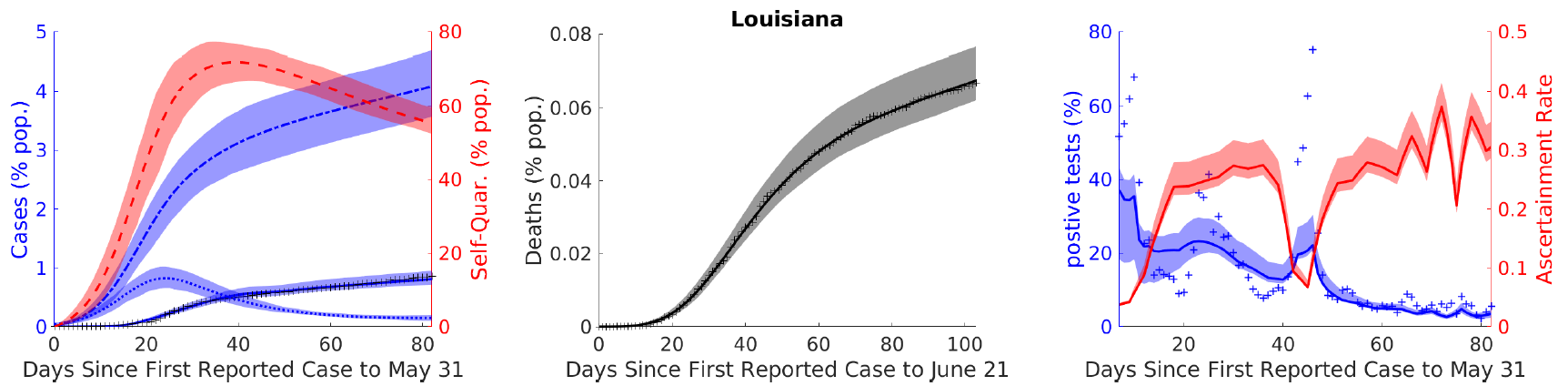
Furthermore, in a study centered on the USA, by incorporating testing data, they were able to explore models for all 55 states and territories. This allowed them to correlate outbreak severity with first wave intervention attributes and suggested potential management strategies for future outbreaks. These results emphasize the criticality of lockdown speed, but also suggest a sufficient population quarantine "half-life duration" of 30 days independent of other model parameters.
Their result on differential impacts of lockdowns and contact tracing also identifies distinct metrics for officials to monitor when enacting each type of intervention.
For reactive lockdowns, the key measurement is rate of population-wide quarantine compared to incidence or incoming reported cases.
For contact tracing, R_0 may be the important quantity because the final outbreak size is only substantially altered as R_0 becomes closer to 1.
Although they found that extensive lockdowns were a much larger factor in controlling COVID-19 outbreak size, their sensitivity analysis shows that contact tracing did dampen and delay the peak number infected despite its more limited impact on the cumulative count. In this way, contact tracing flattened the incidence curve, easing the strain on limited hospital resources.
A combination of expeditiously enacted contact-based interventions may be the best strategy, where effective contact tracing, along with sustained interventions aimed at reducing transmission (public face mask wearing, social distancing, etc.), can synergistically suppress an outbreak, and reduce the scale of lockdown measures necessary for slowing rapidly rising case numbers.
In terms of insights for management of future rapidly spreading outbreaks Cameron Browne stressed that: "In order to balance economic/social concerns in addition to the purely epidemiological, we suggest a new response to an outbreak compared with those observed in the USA first wave: rapid measured lockdown with intermediate half-life duration of quarantine. This strategy describes implementation of rapid reactive lockdown as soon as possible in conjunction with subsequent wave being detected, lasting at least 30 days before 50% return to normalcy, with the underlying R_0 and public adherence to proper social distancing and mask wearing determining the scale of closures during lockdown (where at-risk or sectors responsible for large-scale spread are preferentially included in quarantine)."
This work is detailed in the articles:
Differential impacts of contact tracing and lockdowns on outbreak size in COVID-19 model applied to China which appears in Journal of Theoretical Biology; and,
Modeling COVID-19 outbreaks in United States with distinct testing, lockdown speed and fatigue rates which appears in Royal Society Open Science.
The researchers were partially supported by the NSF grant RAPID: Epidemiological and Phylogenetic Models for Contact-Based Control of COVID-19.

